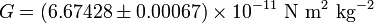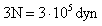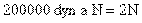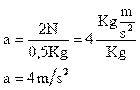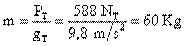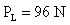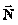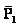Primera ley de Newton o ley de la inercia
Las
leyes de Newton, también conocidas como
leyes del movimiento de Newton, son tres principios a partir de los cuales se explican la mayor parte de los problemas planteados por la
mecanica, en particular, aquellos relativos al movimiento de los cuerpos. Revolucionaron los conceptos básicos de la física y el movimiento de los cuerpos en el universo.
- La primera ley del movimiento rebate la idea aristotélica de que un
cuerpo sólo puede mantenerse en movimiento si se le aplica una fuerza. Newton expone que:
Todo cuerpo persevera en su estado de reposo o movimiento uniforme y
rectilíneo a no ser que sea obligado a cambiar su estado por fuerzas
impresas sobre él.
La formulación original en latín de Newton de esta ley fue:
Corpus omne perseverare in statu suo quiescendi vel movendi
uniformiter in directum, nisi quatenus illud a viribus impressis cogitur
statum suum mutare

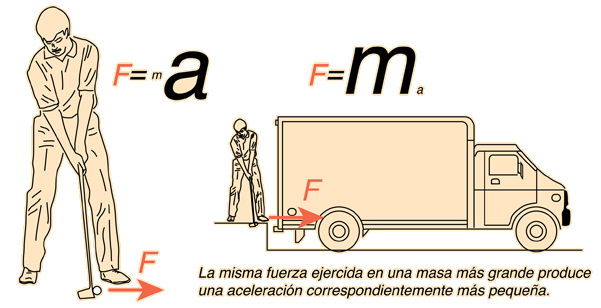
Segunda ley de Newton o ley de fuerza
- La segunda ley del movimiento de Newton dice que:
El cambio de movimiento es proporcional a la fuerza motriz impresa y ocurre según la línea recta a lo largo de la cual aquella fuerza se imprime.
En las palabras originales de Newton:
Mutationem motus proportionalem esse vi motrici impressæ, & fieri secundum lineam rectam qua vis illa imprimitur.
Tercera ley de Newton o ley de acción y reacción
- Con toda acción ocurre siempre una reacción igual y contraria: quiere
decir que las acciones mutuas de dos cuerpos siempre son iguales y
dirigidas en sentido opuesto.
La formulación original de Newton es:
Actioni contrariam semper & æqualem esse reactionem: sive
corporum duorum actiones in se mutuo semper esse æquales & in partes
contrarias dirigi.

La aplicación más importante de la primera
ley de Newton es encontrar el valor de fuerzas que actúan sobre una
partícula, a partir de la condición de
equilibrio.
En la primera ley, se plantea que si una partícula está en equilibrio, se cumple que:
∑F = 0. Como la fuerza es una cantidad vectorial, podemos plantear que:
∑Fx = 0 y ∑Fy = 0 (Componentes rectangulares de las fuerzas).
Ejemplo. Un cuadro de 2 Kg se cuelga de un clavo como se
muestra en la figura, de manera que las cuerdas que lo sostienen forman
un ángulo de 60º.
¿Cuál es la tensión en cada segmento de la cuerda?
Se debe determinar la situación del problema. Una cuerda sostiene un
cuadro de 2 Kg, en dos segmentos, cada segmento tiene una tensión Ta y
Tb respectivamente, como se ilustra en el DCL.
De las tres fuerzas planteadas, solamente se puede determinar el valor de su peso w.
∑Fy = 0 = Ta sen 60º + Tb sen 60º - w;
Ta sen 60º + Tb sen 60º = w = mg (1)
Luego, ∑Fx = 0 = - Ta cos 60º + Tb cos 60º
Ta cos 60º = Tb cos 60º, entonces Ta = Tb (2)
Sustituyendo (2) en (1):
2 Tb sen 60º = mg
Despejando Tb:
Como se demuestra en la ecuación (2), las tensiones en los segmentos de cuerda son iguales.
Ejemplo de problemas relacionados con la Segunda Ley de Newton.
- 1. Una fuerza le proporciona a la masa de 2,5 Kg. una aceleración de
1,2 m/s2. Calcular la magnitud de dicha fuerza en Newton y dinas.
Datos
m = 2,5 Kg.
a =1,2 m/s2.
F =? (N y dyn)
Solución
Nótese que los datos aparecen en un mismo sistema de unidades (M.K.S.)
Para calcular la fuerza usamos la ecuación de la segunda ley de Newton:
 Sustituyendo valores tenemos:
Sustituyendo valores tenemos:
Como nos piden que lo expresemos en dinas, bastará con multiplicar por 105, luego:
- 2. ¿Qué aceleración adquirirá un cuerpo de 0,5 Kg. cuando sobre él actúa una fuerza de 200000 dinas?
Datos
a =?
m = 2,5 Kg.
F = 200000 dyn
Solución
La masa está dada en M.K.S., en cambio la fuerza está dada en c.g.s.
Para trabajar con M.K.S. debemos transformar la fuerza a la unida M.K.S. de esa magnitud (N)

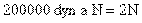
La ecuación de la segunda ley de Newton viene dada por:

Despejando
a tenemos:

Sustituyendo sus valores se tiene:
- 3. Un cuerpo pesa en la tierra 60 Kp. ¿Cuál será a su peso en la luna, donde la gravedad es 1,6 m/s2?
Datos
PT= 60 Kp = 588 N
PL =?
gL = 1,6 m/s2
Solución
Para calcular el peso en la luna usamos la ecuación
Como no conocemos la masa, la calculamos por la ecuación:
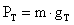
que al despejar
m tenemos:
Esta masa es constante en cualquier parte, por lo que podemos usarla en la ecuación (I):

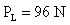
Tercera ley de newton.
- 1. Consideramos un cuerpo con un masa m = 2 Kg. que
está en reposo sobre un plano horizontal, como el indicado en la figura
17. a) Haz un diagrama de cuerpo libre. b) Calcular la fuerza con que
el plano reacciona contra el bloque.

Solución
a) Las fuerzas que actúan sobre el bloque están
representadas en la figura 18, donde se elije un eje de coordenadas cuyo
origen es el centro del cuerpo, mostrándose las fuerzas verticales: el
peso

y la normal
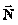
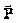
El peso del cuerpo, dirección vertical y sentido hacia abajo.

Normal, fuerza que el plano ejerce sobre el bloque.
Al diagrama así mostrado se le llama
diagrama de cuerpo libre.
b) Para calcular la fuerza que el plano ejerce sobre el bloque aplicamos la segunda ley de Newton:
Como

actúa hacia arriba y
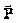
actúa hacia abajo, la resultante viene dada en módulo por N – P, que al aplicar la segunda ley de Newton escribimos:
N – P = m . a
Como en la dirección vertical no hay movimiento entonces la aceleración es cero (a = 0), luego
N – P = 0
N = P
N = m . g (porque P = m ( g)
Sustituyendo los valores de m y g se tiene:
N = 2 Kg . 9,8 m/s2
N = 19,6 N
Esta es la fuerza con que el plano reacciona sobre el bloque.
- 2. En la figura 19 se muestran dos masas M1 = 3 Kg.
y M2 = 5 Kg. colgando de los extremos de un hilo que pasa por la
garganta de una polea a) Hacer un diagrama de las fuerzas que actúan b)
Calcular la tensión del hilo y la aceleración con que se mueve el
sistema.
 Solución
a)
Solución
a) Obsérvese la figura 20(a), la cual representa el diagrama del cuerpo libre para el cuerpo de masa M1.

Es la tensión del hilo, actuando hacia arriba.
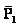
El peso del cuerpo de masa M1.
En la figura 20(b) se muestra el diagrama de cuerpo libre para el cuerpo de masa M2.
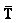
Es la tensión del hilo, actuando hacia arriba.

El peso del cuerpo de masa M2.
b) Como el cuerpo de masa M1 sube, la tensión T es
mayor que P, por lo que podemos escribir en módulo la segunda ley de
Newton así:
T – P1 = M1 . a.………………………………………… (A)
Como el cuerpo de masa M2 baja, el peso P2 es mayor que T, pudiéndose escribir en módulo la segunda ley de Newton así:
P2 – T = M2 . a.………………………………………… (B)
Despajando T de la ecuación (A) nos queda que:
T = M1 . a + P1
Sustituyendo ésta expresión en (B) tenemos:
P2 – (M1 . a + P1) = M2 . a
P2 – P1 = M2 . a + M1 . a
Sacando
a como factor común:
P2 – P1 = a . (M2 + M1)
Despejando nos queda:

(C)
Calculemos por separado P1 y P2
P1 = M1 . g = 3 Kg . 9,8 m/s2
P1 = 29,4 N
P2 = M2 . g = 5 Kg. . 9,8 m/s2
P2 = 49 N
Sustituyendo todos los valores conocidos en la expresión (C) nos queda que:
La tensión la obtenemos sustituyendo en la expresión:
T = M1 . a + P1
T = 3 Kg . 2,45 m/s2 + 29,4 N
T = 7,35 N + 29,4 N
T = 36,4 N
Luego

y T = 36,4 N
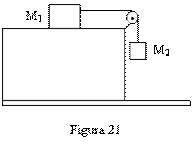
- 3. En la figura 21 se muestran dos bloques de masa
M2 = 2 Kg. que arrastra sobre el plano horizontal al cuerpo de masa M1 =
7 Kg. Calcular la aceleración del sistema y tensión de la cuerda.
 Solución
Solución
Antes debemos hacer un diagrama del cuerpo libre.
Para el bloque horizontal se muestra la figura 21(a) y para el bloque vertical el diagrama de la figura 21(b).

Horizontalmente se desplaza hacia la derecha y la única fuerza que
actúa es la tensión, por lo que puede escribirse de acuerdo con la
segunda ley de Newton que:
T = M1 . a.………………………….…………….….… (I)
En el bloque de masa M2, se lleva a cabo un movimiento vertical hacia abajo, pudiéndose escribir que:
P2 – T = M2 . a.………………………………………… (II)
Sustituyendo T de la ecuación (I) en (II) se tiene:
P2 – M1 . a = M2 ( a
Transponiendo términos se tiene que:
P2 = M2 . a + M1 ( a
Sacando
a como factor común:
P2 = a . (M2 + M1)
Despejando nos queda:

Sustituyendo todos los valores conocidos en la expresión (C) nos queda que:

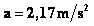
La tensión de la cuerda la obtenemos sustituyendo en la expresión:
T = M1 . a = 2Kg. ( 2,17 m/s2
T = 4,34 N

 y
y  separados una distancia
separados una distancia  es proporcional al producto de sus masas e inversamente proporcional al cuadrado de la distancia, es decir:
es proporcional al producto de sus masas e inversamente proporcional al cuadrado de la distancia, es decir: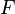 es el módulo de la fuerza ejercida entre ambos cuerpos, y su dirección se encuentra en el eje que une ambos cuerpos.
es el módulo de la fuerza ejercida entre ambos cuerpos, y su dirección se encuentra en el eje que une ambos cuerpos. es la constante de la gravitacion universal
es la constante de la gravitacion universal